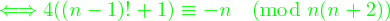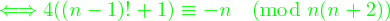双子素数 (1~10000)
(p, p + 2) の両方が素数.
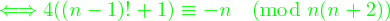
未解決問題 : 双子素数は無限に存在するか?
| (3 , 5) |
(5 , 7) |
(11 , 13) |
(17 , 19) |
(29 , 31) |
(41 , 43) |
(59 , 61) |
(71 , 73) |
(101 , 103) |
(107 , 109) |
| (137 , 139) |
(149 , 151) |
(179 , 181) |
(191 , 193) |
(197 , 199) |
(227 , 229) |
(239 , 241) |
(269 , 271) |
(281 , 283) |
(311 , 313) |
| (347 , 349) |
(419 , 421) |
(431 , 433) |
(461 , 463) |
(521 , 523) |
(569 , 571) |
(599 , 601) |
(617 , 619) |
(641 , 643) |
(659 , 661) |
| (809 , 811) |
(821 , 823) |
(827 , 829) |
(857 , 859) |
(881 , 883) |
(1019 , 1021) |
(1031 , 1033) |
(1049 , 1051) |
(1061 , 1063) |
(1091 , 1093) |
| (1151 , 1153) |
(1229 , 1231) |
(1277 , 1279) |
(1289 , 1291) |
(1301 , 1303) |
(1319 , 1321) |
(1427 , 1429) |
(1451 , 1453) |
(1481 , 1483) |
(1487 , 1489) |
| (1607 , 1609) |
(1619 , 1621) |
(1667 , 1669) |
(1697 , 1699) |
(1721 , 1723) |
(1787 , 1789) |
(1871 , 1873) |
(1877 , 1879) |
(1931 , 1933) |
(1949 , 1951) |
| (1997 , 1999) |
(2027 , 2029) |
(2081 , 2083) |
(2087 , 2089) |
(2111 , 2113) |
(2129 , 2131) |
(2141 , 2143) |
(2237 , 2239) |
(2267 , 2269) |
(2309 , 2311) |
| (2339 , 2341) |
(2381 , 2383) |
(2549 , 2551) |
(2591 , 2593) |
(2657 , 2659) |
(2687 , 2689) |
(2711 , 2713) |
(2729 , 2731) |
(2789 , 2791) |
(2801 , 2803) |
| (2969 , 2971) |
(2999 , 3001) |
(3119 , 3121) |
(3167 , 3169) |
(3251 , 3253) |
(3257 , 3259) |
(3299 , 3301) |
(3329 , 3331) |
(3359 , 3361) |
(3371 , 3373) |
| (3389 , 3391) |
(3461 , 3463) |
(3467 , 3469) |
(3527 , 3529) |
(3539 , 3541) |
(3557 , 3559) |
(3581 , 3583) |
(3671 , 3673) |
(3767 , 3769) |
(3821 , 3823) |
| (3851 , 3853) |
(3917 , 3919) |
(3929 , 3931) |
(4001 , 4003) |
(4019 , 4021) |
(4049 , 4051) |
(4091 , 4093) |
(4127 , 4129) |
(4157 , 4159) |
(4217 , 4219) |
| (4229 , 4231) |
(4241 , 4243) |
(4259 , 4261) |
(4271 , 4273) |
(4337 , 4339) |
(4421 , 4423) |
(4481 , 4483) |
(4517 , 4519) |
(4547 , 4549) |
(4637 , 4639) |
| (4649 , 4651) |
(4721 , 4723) |
(4787 , 4789) |
(4799 , 4801) |
(4931 , 4933) |
(4967 , 4969) |
(5009 , 5011) |
(5021 , 5023) |
(5099 , 5101) |
(5231 , 5233) |
| (5279 , 5281) |
(5417 , 5419) |
(5441 , 5443) |
(5477 , 5479) |
(5501 , 5503) |
(5519 , 5521) |
(5639 , 5641) |
(5651 , 5653) |
(5657 , 5659) |
(5741 , 5743) |
| (5849 , 5851) |
(5867 , 5869) |
(5879 , 5881) |
(6089 , 6091) |
(6131 , 6133) |
(6197 , 6199) |
(6269 , 6271) |
(6299 , 6301) |
(6359 , 6361) |
(6449 , 6451) |
| (6551 , 6553) |
(6569 , 6571) |
(6659 , 6661) |
(6689 , 6691) |
(6701 , 6703) |
(6761 , 6763) |
(6779 , 6781) |
(6791 , 6793) |
(6827 , 6829) |
(6869 , 6871) |
| (6947 , 6949) |
(6959 , 6961) |
(7127 , 7129) |
(7211 , 7213) |
(7307 , 7309) |
(7331 , 7333) |
(7349 , 7351) |
(7457 , 7459) |
(7487 , 7489) |
(7547 , 7549) |
| (7559 , 7561) |
(7589 , 7591) |
(7757 , 7759) |
(7877 , 7879) |
(7949 , 7951) |
(8009 , 8011) |
(8087 , 8089) |
(8219 , 8221) |
(8231 , 8233) |
(8291 , 8293) |
| (8387 , 8389) |
(8429 , 8431) |
(8537 , 8539) |
(8597 , 8599) |
(8627 , 8629) |
(8819 , 8821) |
(8837 , 8839) |
(8861 , 8863) |
(8969 , 8971) |
(8999 , 9001) |
| (9011 , 9013) |
(9041 , 9043) |
(9239 , 9241) |
(9281 , 9283) |
(9341 , 9343) |
(9419 , 9421) |
(9431 , 9433) |
(9437 , 9439) |
(9461 , 9463) |
(9629 , 9631) |
| (9677 , 9679) |
(9719 , 9721) |
(9767 , 9769) |
(9857 , 9859) |
(9929 , 9931) |
|
|
|
|
|